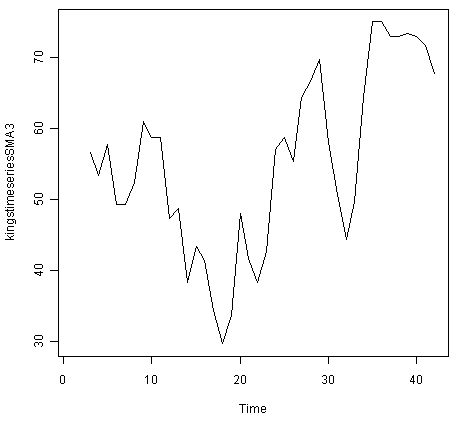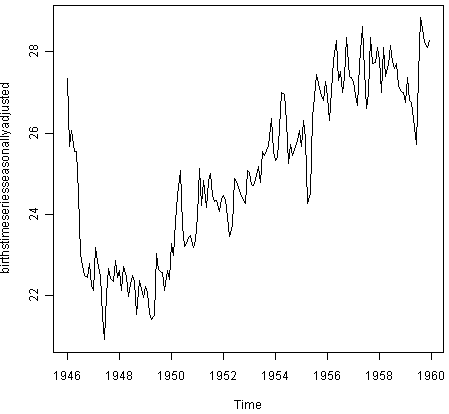Проект Templet

Перевод статьи: http://a-little-book-of-r-for-time-series.readthedocs.org/en/latest/src/timeseries.html

Автор: Avril Coghlan

Перевод: Артамонов Юрий

Эта статья расскажет вам как использовать R - статистическое ПО для выполнения некоторых простых действий анализа данных, которые распространены при анализе временных рядов.

Эта статья предполагает, что читатель имеет некоторые базовые знания об анализе временных рядов, и основная цель статьи не рассмотреть анализ временных рядов, а объяснить, как выполнять анализ, используя R.

Если вы новичок в анализе временных рядов, и хотите узнать больше о любой из концепций, представленных здесь, я очень рекомендую книгу Open University «Time series» (код продукта M249 / 02), доступный в магазине Open University.

В этой статье я буду использовать наборы данных, которые любезно предоставил Роб Гайдман в своей библиотеке Time Series Data Library http://robjhyndman.com/TSDL/.

Первое, что вы захотите сделать, чтобы проанализировать данные вашего временного ряда, это прочитать их в R и вывести временной ряд на экран. Вы можете считать данные в R, используя функцию scan(), которая предполагает, что ваши данные для последовательных моментов времени это простой текстовый файл с одной колонкой.

Например, файл http://robjhyndman.com/tsdldata/misc/kings.dat содержит данные годов жизни королей Англии последовательно, начиная с Вильяма Завоевателя (Оригинальный источник: Hipel and Mcleod, 1994)

Данные выглядят так:

kings.dat

Age of Death of Successive Kings of England
#starting with William the Conqueror
#Source: McNeill, "Interactive Data Analysis"
60
43
67
50
56
42
50
65
68
43
65
34
...

Показаны только несколько первых строк файла. Первые 3 строки содержат некоторые комментарии относительно данных, и мы хотим их игнорировать при считывании строк в R. Мы можем указать это, используя параметр skip функции scan(), который определяет сколько строк игнорировать с начала файла. Для чтения файла в R с игнорированием первых 3 строк мы набираем:

> kings <- scan("http://robjhyndman.com/tsdldata/misc/kings.dat",skip=3)
  Read 42 items
> kings
  [1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59 48
  [26] 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56

В этом случае возраст смерти 42 королей Англии был прочитан в переменную kings.

После того, как мы прочитали данные в R, мы будем хранить данные в объекте типа временной ряд, так что мы сможем использовать множество функций R для анализа данных временных рядов. Для хранения данных в объекте временного ряда мы используем функцию ts(). Например, для хранения данных в переменной kings в качестве объекта временного ряда мы набираем:

> kingstimeseries <- ts(kings)
> kingstimeseries
  Time Series:
  Start = 1
  End = 42
  Frequency = 1
  [1] 60 43 67 50 56 42 50 65 68 43 65 34 47 34 49 41 13 35 53 56 16 43 69 59 48
  [26] 59 86 55 68 51 33 49 67 77 81 67 71 81 68 70 77 56

Иногда набор данных временного ряда, который у вас есть, мог быть собран на регулярных интервалах меньших чем один год, например, по месяцам или кварталам. В этом случае вы моежет указать количество измерений сделанных за год, используя параметр frequency функции ts(). Для временных рядов по месяцам вы установите frequency=12, а для данных по кварталам frequency=4.

Вы также можете указать первый год, в который собирались данные, и первый интервал в году с помощью параметра start функции ts(). Например, если первая точка данных соответствует второму кварталу 1986 года, вы должны установить start=c(1986,2).

Примером может служить набор данных о количестве рождений в месяц в Нью-Йорке, с января 1946 по декабрь 1959 (первоначально собраны Ньютоном). Эти данные доступны в файле http://robjhyndman.com/tsdldata/data/nybirths.dat. Мы можем прочитать данные и сохранить их в объекте временного ряда, набрав:

> births <- scan("http://robjhyndman.com/tsdldata/data/nybirths.dat")
  Read 168 items
> birthstimeseries <- ts(births, frequency=12, start=c(1946,1))
> birthstimeseries
       Jan    Feb    Mar    Apr    May    Jun    Jul    Aug    Sep    Oct    Nov    Dec
  1946 26.663 23.598 26.931 24.740 25.806 24.364 24.477 23.901 23.175 23.227 21.672 21.870
  1947 21.439 21.089 23.709 21.669 21.752 20.761 23.479 23.824 23.105 23.110 21.759 22.073
  1948 21.937 20.035 23.590 21.672 22.222 22.123 23.950 23.504 22.238 23.142 21.059 21.573
  1949 21.548 20.000 22.424 20.615 21.761 22.874 24.104 23.748 23.262 22.907 21.519 22.025
  1950 22.604 20.894 24.677 23.673 25.320 23.583 24.671 24.454 24.122 24.252 22.084 22.991
  1951 23.287 23.049 25.076 24.037 24.430 24.667 26.451 25.618 25.014 25.110 22.964 23.981
  1952 23.798 22.270 24.775 22.646 23.988 24.737 26.276 25.816 25.210 25.199 23.162 24.707
  1953 24.364 22.644 25.565 24.062 25.431 24.635 27.009 26.606 26.268 26.462 25.246 25.180
  1954 24.657 23.304 26.982 26.199 27.210 26.122 26.706 26.878 26.152 26.379 24.712 25.688
  1955 24.990 24.239 26.721 23.475 24.767 26.219 28.361 28.599 27.914 27.784 25.693 26.881
  1956 26.217 24.218 27.914 26.975 28.527 27.139 28.982 28.169 28.056 29.136 26.291 26.987
  1957 26.589 24.848 27.543 26.896 28.878 27.390 28.065 28.141 29.048 28.484 26.634 27.735
  1958 27.132 24.924 28.963 26.589 27.931 28.009 29.229 28.759 28.405 27.945 25.912 26.619
  1959 26.076 25.286 27.660 25.951 26.398 25.565 28.865 30.000 29.261 29.012 26.992 27.897

Похожим образом, файл http://robjhyndman.com/tsdldata/data/fancy.dat содержит ежемесячные продажи сувенирного магазина на пляже курортного городка в штате Квинсленд Австралия с января 1987 по декабрь 1993 года (исходные данные Wheelwright and Hyndman 1998). Мы можем считать данные, напечатав:

> souvenir <- scan("http://robjhyndman.com/tsdldata/data/fancy.dat")
  Read 84 items
> souvenirtimeseries <- ts(souvenir, frequency=12, start=c(1987,1))
> souvenirtimeseries
         Jan       Feb       Mar       Apr       May       Jun       Jul       Aug       Sep       Oct       Nov      Dec
  1987   1664.81   2397.53   2840.71   3547.29   3752.96   3714.74   4349.61   3566.34   5021.82   6423.48   7600.60  19756.21
  1988   2499.81   5198.24   7225.14   4806.03   5900.88   4951.34   6179.12   4752.15   5496.43   5835.10  12600.08  28541.72
  1989   4717.02   5702.63   9957.58   5304.78   6492.43   6630.80   7349.62   8176.62   8573.17   9690.50  15151.84  34061.01
  1990   5921.10   5814.58  12421.25   6369.77   7609.12   7224.75   8121.22   7979.25   8093.06   8476.70  17914.66  30114.41
  1991   4826.64   6470.23   9638.77   8821.17   8722.37  10209.48  11276.55  12552.22  11637.39  13606.89  21822.11  45060.69
  1992   7615.03   9849.69  14558.40  11587.33   9332.56  13082.09  16732.78  19888.61  23933.38  25391.35  36024.80  80721.71
  1993  10243.24  11266.88  21826.84  17357.33  15997.79  18601.53  26155.15  28586.52  30505.41  30821.33  46634.38 104660.67

После того, как вы прочли данные временного ряда, следующим шагом, как правило, вы построите график данные ряда при помощи функции plot.ts().

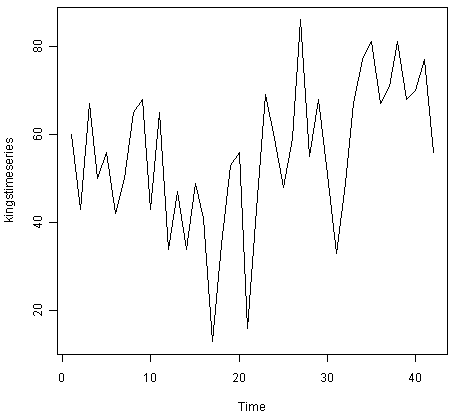
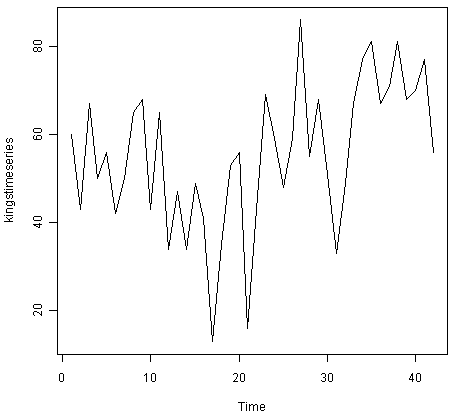
Например, чтобы построить график временного ряда возраста смерти 42 королей Англии, мы введём:

> plot.ts(kingstimeseries)

Мы можем видеть из графика, что временной ряд, вероятно, может быть описан при помощи аддитивной модели, поскольку случайные флуктации в данных примерно постоянны с течением времени.

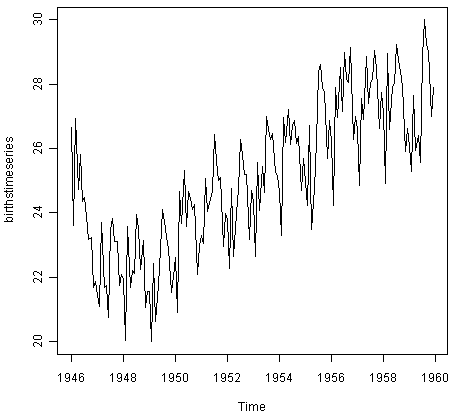
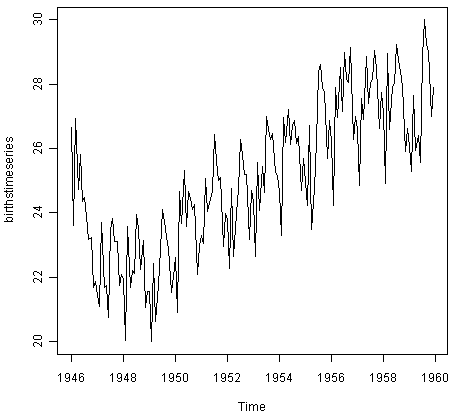
Похожим образом, для построения графика временного ряда числа рождений в месяц в Нью-Йорке мы введём:

> plot.ts(birthstimeseries)

Мы можем заметить, что есть сезонные колебания в числе рождений в месяц: есть пик каждое лето и дно каждую зиму. Опять же, похоже временной ряд может быть описан аддитивной моделью, поскольку сезонные колебания примерно постоянны с течением времени и, кажется, не зависят от уровня временного ряда, и случайные колебания также примерно постоянны по значению в течение долгого времени.

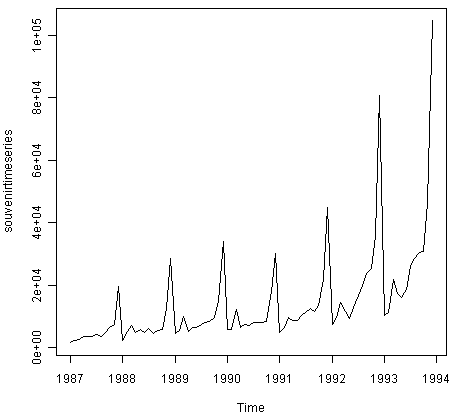
Для построения графика ряда ежемесячных продаж в магазине сувениров на пляже курортного городка в штате Квинсленд Австралии мы используем такой код:

> plot.ts(souvenirtimeseries)

В этом случае, очевидно, что аддитивная модель не подходит для описания временного ряда, так как размер сезонных колебаний и случайные флуктации возрастают с увеличением уровня временного ряда. Таким образом, нам, возможно, потребуется преобразовать временной ряд для того, чтобы получить некоторый ряд, который можно описать с использованием аддитивной модели. Например, мы можем преобразовать временной ряд, вычислив натуральный логарифм от начальных данных:

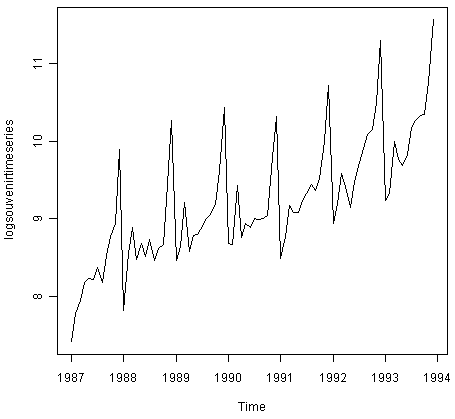
> logsouvenirtimeseries <- log(souvenirtimeseries)
> plot.ts(logsouvenirtimeseries)

Здесь мы видим, что величина сезонных колебаний и случайных колебаний в лог-преобразованном временном ряде примерно постоянны в течение долгого времени, и не зависят от уровня временного ряда. Таким образом, лог-преобразованный временной ряд, вероятно, может быть описан с использованием аддитивной модели.

Разложение временного ряда - разделение его на составляющие компоненты, обычно это тренд и нерегулярная составляющая, и если это периодический ряд, сезонная компонента.

Непериодический временной ряд состоит из составляющей тренда и нерегулярной компоненты. Разложение временного ряда сопряжено с попытками разделить временной ряд на эти компоненты, то есть, оценить трендовую составляющую и нерегулярную составляющую.

Для оценки трендовой составляющей в непериодических временных рядах, которые могут быть описаны аддитивной моделью, часто используется метод сглаживания, например, вычислением простого скользящего среднего.

Функция SMA() пакета «TTR» может быть использована для сглаживания временного ряда при помощи скользящего среднего. Для использования этой функции нам необходимо установить пакет «TTR» (инструкции по установки пакетов R смотри How to install an R package). Как только вы установили пакет «TTR», вы можете загрузить пакет «TTR» введя:

> library("TTR")

Затем вы можете использовать функцию SMA() для сглаживания данных временного ряда. Для использования функции SMA() вам необходимо указать порядок (ширину) простого скользящего среднего, используя параметр n. Например, чтобы вычислить простое скользящее среднее порядка 5, мы устанавливаем n=5 в функции SMA.

Например, как обсуждалось выше, временной ряд годов смерти 42 королей Англии не является периодическим, и, вероятно, может быть описана аддитивной моделью, поскольку случайные флуктации в данных, по грубому приближению, постоянны по всей выборке:

Так, мы можем попробовать оценить составляющую тренда этого временного ряда при сглаживании его простым скользящим средним. Для сглаживания временного ряда используем простое скользящее среднее порядка 3 и выведем результирующий график:

> kingstimeseriesSMA3 <- SMA(kingstimeseries,n=3)
> plot.ts(kingstimeseriesSMA3)

Похоже, множество случайных флуктаций всё ещё проявляется во временном ряде, сглаженном при помощи простого скользящего среднего порядка 3. Так, для оценки составляющей тренда с большей точностью мы можем захотеть попробовать сглаживание данных простым скользящим средним большего порядка. Поиск правильного порядка для сглаживания потребует небольшого числа проб и ошибок. Например, мы можем попробовать использовать простое скользящее среднее порядка 8.

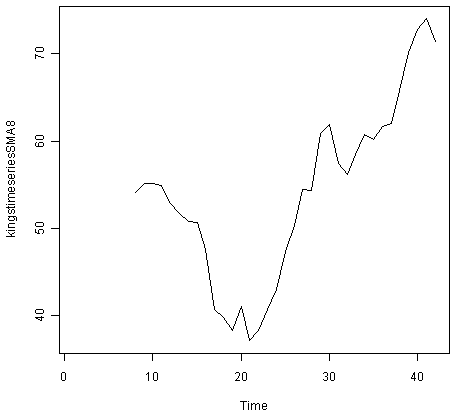
> kingstimeseriesSMA8 <- SMA(kingstimeseries,n=8)
> plot.ts(kingstimeseriesSMA8)

Данные, сглаженные при помощи простого скользящего среднего порядка 8, дают прозрачную картину составляющей тренда и мы можем видеть, что продолжительность жизни королей, вероятно, снижалась с примерно 55 лет до примерно 38 лет в период первых 20 королей, а затем увеличивалась до 73 лет к концу правления 40ого короля во временном ряду.

Периодические данные состоят из составляющей тренда, периодической составляющей и нерегулярной составляющей. Разложение временного ряда - разделение этого временного ряда на эти 3 компоненты, то есть оценка этих составляющих.

Чтобы оценить составляющую тренда и периодическую составляющую периодического временного ряда, который может быть описан аддитивной моделью, мы можем использовать функцию decompose(). Это функция оценивает тренд, периодическую и нерегулярную составляющие временного ряда, который может быть описан аддитивной моделью.

Функиция decompose() возвращает список объектов в качестве результата, где содержатся оценки периодической составляющей, тренда и нерегулярной компоненты, хранящиеся в именованых элементах этого списка объектов, называемых «seasonal», «trend» и «random» соответственно.

Например, как было рассмотрено ранее, временной ряд количества новорожденных по месяца в Нью Йорке - периодический, с пиком каждое лето и провалом каждую зиму, вероятно может быть описан с использованием аддтивной модели, поскольку периодические и случайные флуктации, на первый взгляда, постоянны по величине во времени:

Для оценки тренда, периодической и нерегулярной составляющей этого временного ряда мы вводим:

> birthstimeseriescomponents <- decompose(birthstimeseries)

Оценки значений тренда, периодической и нерегулярной компоненты будут сохранены в переменных birthstimeseriescomponents$seasonal, birthstimeseriescomponents$trend и birthstimeseriescomponents$random. Например, мы можем вывести оценки значений сезонной компоненты напечатав:

> birthstimeseriescomponents$seasonal # get the estimated values of the seasonal component
       Jan        Feb        Mar        Apr        May        Jun        Jul        Aug        Sep        Oct        Nov        Dec
 1946 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1947 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1948 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1949 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1950 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1951 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1952 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1953 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1954 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1955 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1956 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1957 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1958 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197
 1959 -0.6771947 -2.0829607  0.8625232 -0.8016787  0.2516514 -0.1532556  1.4560457  1.1645938  0.6916162  0.7752444 -1.1097652 -0.3768197

Оценки значений сезонной компоненты приведены для месяцев с января по декабрь для каждого года. Наиюольшее значение сезонной составляющей в июле (примерно 1.46), а наименьшее в февреле (примерно -2.08), что соответствует пику рождаемости в июле и провалу в феврале каждого года.

Мы можем вывести оценки тренда, сеознной и нерегулярной компоненты временного ряда используя функцию plot(), например так:

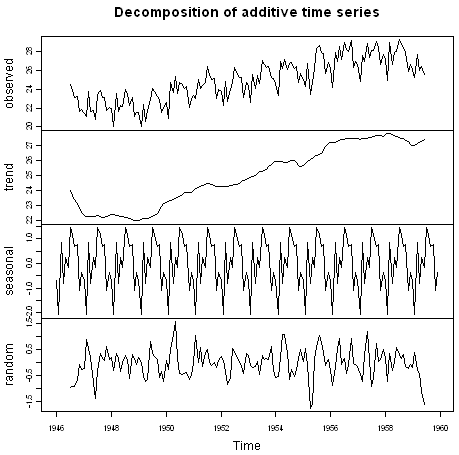
> plot(birthstimeseriescomponents)

На графиках выше показан исходный временной ряд (верхний график), оценка составляющей тренда(второй сверху), оценка сезонной компоненты(третий сверху) и оценка случайной компоненты(последний). Мы видим, что оценка тренда немного уменьшилась с 24 в 1947 до 22 в 1948, а затем неуклонно росла примерно до 27 в 1959.

Если у вас есть периодический временной ряд, который может быть описан аддитивной моделью, вы можете исключить сезонную компоненту, вычтя оценку сезонной компоненты из исходного временного ряда. Мы можем сделать это, используя оценку сезонной компоненты, вычисленной функцией decompose().

Например, для исключения сезонной составляющей временного ряда количества рождений по месяцам в Нью Йорке мы можем оценить сезонную составляющую, используя decompose(), и затем вычесть сезонную компоненту из исходного временного ряда:

> birthstimeseriescomponents <- decompose(birthstimeseries)
> birthstimeseriesseasonallyadjusted <- birthstimeseries - birthstimeseriescomponents$seasonal

Затем мы можем вывести график временного ряда без сезонной составляющей при помощи функции plot():

> plot(birthstimeseriesseasonallyadjusted)

На графике видно, что сезонные перепады были удалены из исходного временного ряда. Получившийся временной ряд содержит только составляющую тренда и нерегулярную составляющую.

Экспоненциальное сглаживание может быть использовано для краткосрочных прогнозов данных временного ряда.

Если ваш временной ряд может быть описан аддтивной моделью с постоянным уровнем и не содержит сезонных колебаний, вы можете использовать простое экспоненциальное сглаживание для краткосрочного прогнозирования.

Простое экспоненциальное сглаживание даёт возможность оценить уровень в текущей точке. Сглаживание определяется параметром alpha, изменяющимся в диапазоне от 0 до 1. Значения alpha, которые близки к 0 означают, что более старым наблюдениям в истории будут присвоены меньшие веса при прогнозировании будущих значений.

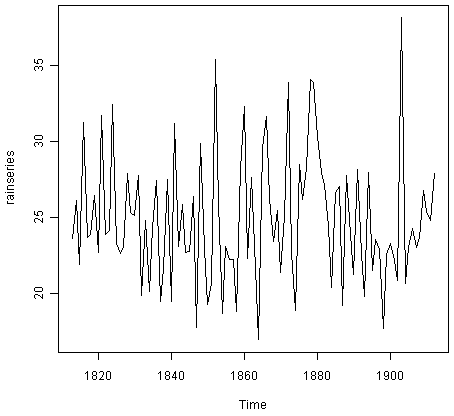
Например, файл http://robjhyndman.com/tsdldata/hurst/precip1.dat содержит общее годовое количество осадков в дюймах в Лондоне за период 1813-1912 г. (исходные данные из Hipel and McLeod, 1994). Мы можем прочитать данне в R и вывести их при помощи команды:

> rain <- scan("http://robjhyndman.com/tsdldata/hurst/precip1.dat",skip=1)
  Read 100 items
> rainseries <- ts(rain,start=c(1813))
> plot.ts(rainseries)

Как видно из графика, уровень остаётся примерно постоянным (среднее значение остаётся постоянным на уровне 25 дюймов). Случайные отклонения во временном ряде примерно постоянны по значению, так что, вероятно, мы можем описать данные используя аддитивную модель. То есть, мы можем прогнозировать при помощи простого экспоненциального сглаживания.

Для прогнозирования при помощи простого экспоненциального сглаживания в R, мы можем использовать модель прогноза простого экспоненциального сглаживания при помощи функции HoltWinters(). Чтобы использовать HoltWinters() для простого экспоненциального сглаживания, мы должны установить параметр beta=FALSE и gamma=FALSE в функции HoltWinters() (параметры beta и gamma используются в экспоненциальном сглаживании Хольта и в экспоненциальном сглаживании Хольта-Винтера, как описывается ниже).

Функция HoltWinters() возвращает список переменных, которые содержат именованные элементы.

Например, чтобы использовать простое экспоненциальное сглаживание для прогнозирования значений временного ряда годовых осадков в Лондоне, мы введём:

> rainseriesforecasts <- HoltWinters(rainseries, beta=FALSE, gamma=FALSE)
> rainseriesforecasts
  Smoothing parameters:
  alpha:  0.02412151
  beta :  FALSE
  gamma:  FALSE
  Coefficients:
    [,1]
  a 24.67819

Вывод функции HoltWinters() сообщает нам, что оценка значения параметра alpha примерно 0.024. Это очень близко к 0, что говорит нам, что прогноз основан на более поздних значениях и в меньшей степени на ранних значениях.

По умолчанию, HoltWinters() делает прогноз только для того же периода времени, что и в исходном временном ряду. В это случае, исходный временной ряд включает осадки в Лондоне за 1813-1912, так что прогноз тоже для периода 1813-1912.

TODO

TODO

TODO